Section I-C: Kinetic Energy
Calculating the kinetic energy of a projectile is fairly straight forward using the following equation:
KE = 1/2 m * v 2
where m is the mass of the projectile in kilograms, and v is the velocity in meters per second.
In Airsoft, energy is unimportant in calculating trajectory, however it is very important when determining safe minimum engagement distances (or MED's). In terminal ballistics, the impact energy in relation to impact area is ultimately what determines whether or not a projectile will penetrate a given target. In the UK, for instance, they've determined that an impact greater than 1.35 Joules (with 6mm Projectiles) is capable of serious harm (though I have been unable to find further specifics on this). To further ensure safety, the recommended minimum engagement distances in this study (see Section VI-C: Recommended Universal MED's) allow for a maximum impact energy no greater than 1.00 Joule.
For example, a 0.25g 6mm BB fired at 358 fps would have a muzzle energy of 1.49 Joules, calculated as follows:
KE = 1/2 m * v 2 = 0.5 * 0.00025 kg * 109 m/s2 = 1.49 kg * m2/s2 = 1.49 Joules
As the BB encounters drag throughout its trajectory, its velocity diminishes, as shown in Figure I-C-01:
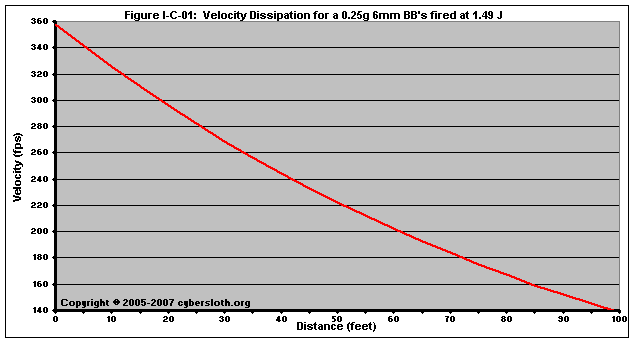
As velocity decreases, so to does the kinetic energy. In order for a BB to have a safe impact, its velocity will need to decrease to the point where its kinetic energy is less than 1.00 Joules. A 0.25g BB will have 1.00 J of energy at 293 fps. From the above chart, we can see that the BB's velocity will reach 293 fps at a range of roughly 21 feet. This is further illustrated in Figure I-C-02, wherein we can see that, at a distance of about 21 feet, the 0.25g BB has reached the 1.00 J mark:
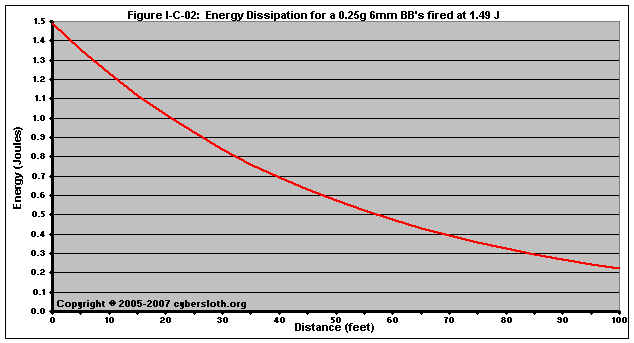
Most rifles below 1.5 J are fairly uniform in terms of muzzle energy. In other words, a stock rifle that fires a 0.20g BB at 0.75 J will probably fire a 0.25g BB at 0.75 J. To keep the energy the same, a heavier BB will need to be moving slower. A rifle with a muzzle energy of 0.75 J would fire 0.20g BB's at 285 fps, and it would fire 0.25 g BB's at 255 fps. (To calculate velocities for an equal energy, see Section X-B: Relative Energy / MED Calculator.)
For rifles above 1.5 J, muzzle energy is not always constant for different masses. As is explained in Section VI-A: Determining Muzzle Energy, lighter BB's in high-energy rifles are -- particularly gas rifles -- sometimes exit the barrel before they have had a chance absorb all of the energy from the spring compression or gas expansion. This is not true for all high-energy rifles, but occurs often enough to be worth noting.
One of the more interesting things, something of particular importance when determining MED's, is that for equal muzzle energies, heavier BB's dissipate energy at a slower rate. There are two reasons for this. First, for equal muzzle energies, a lighter BB will be moving faster than a heavier one. As you will see in Section I-D-01: Drag Force, drag increases with the square of the velocity. A BB moving at 400 fps, for example, will experience considerably more drag than a BB moving at 300 fps. The second reason that heavier BB's dissipate energy at a slower rate is that the deceleration a BB experiences is inversely proportional to the mass of the BB. As the mass increases, the rate of deceleration decreases.
The sum of these reasons can be seen in the Energy Dissipation plot in Figure I-C-03:
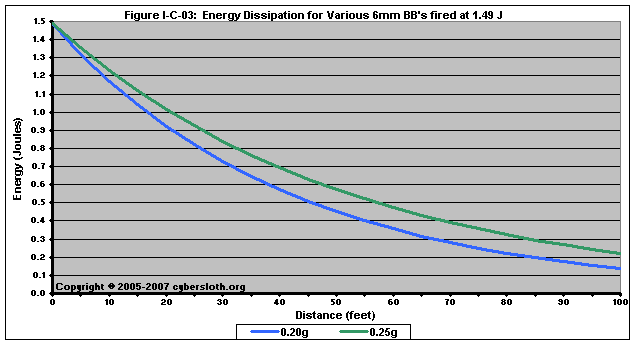
If we were to use this plot to obtain safe engagement distance (again, determined as the point at which the BB has less than 1.00 J of kinetic energy), we can see that the 0.20g BB would need an MED of about 17 feet, while the 0.25g BB needs an MED of about 21 feet. This may not seem significant, however when talking about rifles with very high muzzle energies, the discrepancy in MED between BB's of different masses becomes tremendous.
Figure I-C-04 depicts three BB's all fired at the same muzzle energy of 3.35 J, the equivalent of 600 fps with 0.20g BB's:
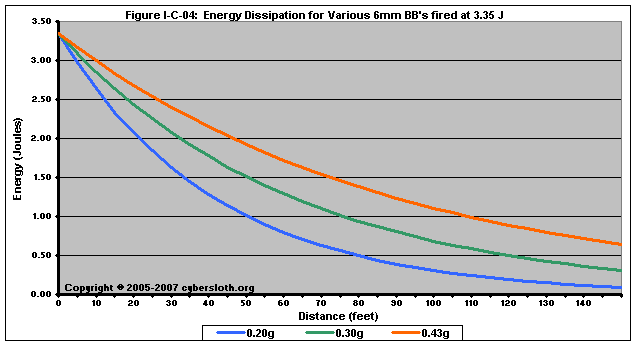
In this case, the 0.20g BB will have dissipated enough energy such that it is safe at a distance of about 51 feet, while the 0.30g and 0.43g BB's have reached a safe energy at a distance of about 76 feet and about 109 feet, respectively. The significance of this is discussed in great detail in Section VI-C: Recommended Universal MED's.
Another example is to look at muzzle energies that require an MED of 60 feet, as depicted in Figure I-C-05. Again, the impact energy depends as much upon the weight of the ammunition used as it does muzzle energy.
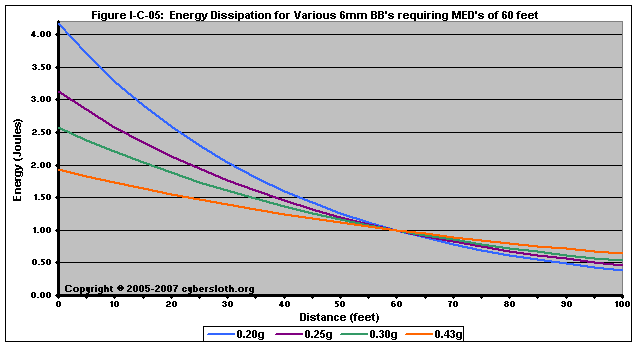
To put those numbers into context, let's look at what the values correspond to when it comes to the chronograph.
| Weight of Ammo to be Used | 0.20g | 0.25g | 0.30g | 0.43g | |
| Muzzle Energy (Joules) | 4.2 | 3.1 | 2.6 | 1.9 | |
| Chrono Velocity w/ 0.20g BB's | 670 | 580 | 527 | 456 | |
| Velocity for Given Ammo | 670 | 519 | 430 | 311 | |
| MED Required | 60 | 60 | 60 | 60 |
If a person arrived at a site with a rifle that chronos at 550 fps (w/ 0.20g BB's) and plans to use 0.30g BB's at the match, he or she would more than likely be turned away. If another person arrived with a rifle that chronos at 480 fps (w/ 0.20g BB's) and plans on using 0.43g BB's during the match, according to many site's rules, he or she would be allowed. In reality, the person who's rifle chrono'd at the higher velocity (550 / 0.20) would actually be safer on the field due to the weight of the ammo being used (0.30g).
The point is, and it is nonnutritive yet very important, is that when determining velocity limits and MED's, it is just as important to restrict ammunition weight as it is to restrict muzzle velocity. At our site, we found it more important to raise the velocity limits used by snipers and instead place a hard restriction on the weight of the ammunition used (anything over 0.30g is not allowed).
Another note of interest is that drag is affected by the size of the projectile -- specifically its orthogonal, or cross-sectional area -- such that the force of drag increases directly proportional the increase in frontal area. It makes sense, then, to realize that 8mm BB's will experience greater drag when compared to 6mm BB's at equal mass and velocity.
Figure I-C-06 shows the energy dissipation for 8mm BB's of nearly equal mass:
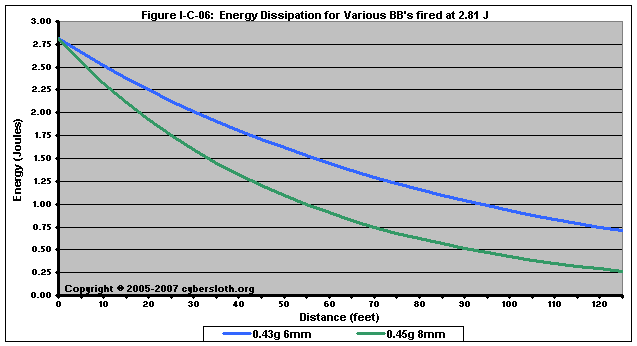
2.81 Joules, a muzzle energy equal to 550 fps with a 0.20g BB, corresponds to a muzzle velocity of 375 fps with the 0.43g 6mm BB and 367 fps with the 0.45g 8mm BB. Even though the 8mm BB is slightly heavier, it ultimately dissipates its energy at a considerably faster rate than the 6mm BB. In terms of safe engagement distances, the 6mm BB would need an MED of about 94 feet, whereas the 8mm BB would only need an MED of 57 feet.
Figure I-C-07 depicts the energy dissipation for various BB's, all fired at 1.49 Joules (the equivalent of 400 fps with 0.20g BB's):
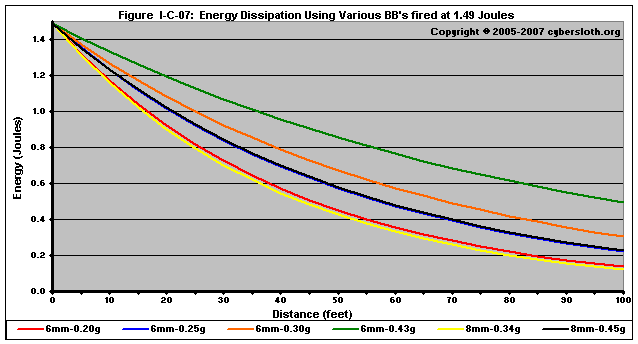
Notice that the 0.43g 6mm BB retains its energy best. The 8mm BB's dissipate energy at a rate similar to that of significantly lighter 6mm BB's.
Comparing the 6mm BB's to 8mm BB's, we see that 0.34g 8mm BB's dissipate energy at about the same rate as 0.20g 6mm BB's, and 0.45g 8mm BB's dissipate energy at about the same rate as 0.25g 6mm BB's (the 0.25g 6mm BB line is hard to see as it is overlapped by the 0.45g 8mm BB line). And all four of those BB's dissipate energy faster than any of the heavier 6mm BB's (>0.26g). It might seem as though density is the governing factor for why certain BB's dissipate energy faster than others. However, there is no direct-correlation between energy dissipation and density. Rather, energy dissipation is related to velocity dissipation, which is a function of initial velocity, frontal area, and mass.
One additional point concerning 8mm BB's is that their inherently safer than 6mm BB's at equal impact energies. This goes back to the original statement that it is the impact energy in relation to impact area is ultimately what determines whether or not a projectile will penetrate a given target. By increasing impact area (and an 8mm BB has nearly twice the impact area of a 6mm BB), the impact energy is distributed over a larger area. To many, this seems counterintuitive but it explained in further detail in Section VI-B: Safe Impact Energy.