Section III: Effects of Hop-Up
Friction interaction between the hop-up bucking and pellet incur a backspin upon the pellet. This backspin induces force orthogonal to the pellet's motion due a special condition of Bernoulli's Principle known as the Magnus Effect. The Magnus Effect is due to the high-speed interaction between the pellet and the surrounding air. (For simplicity, spin hereafter refers particularly to backspin.)
There is often debate over which force is more so responsible for the effect of lift, Bernoulli's Principle or the Magnus Effect. Technically, Bernoulli's Principle deals with low pressure due to an object moving over a medium at high speed (or the medium moving over the object). Magnus Lift is more accurately attributed to the momentum shift of the boundary-layer due to variable areas of low pressure around the object, the effect of which causes a net movement of the object in the direction opposite of the motion of the boundary layer. Both cause lift on the BB's, however the effects of each are significantly dependent upon 1) the speed of the object through a medium, and 2) the rotational velocity of the object.
When a relatively smooth, spherical object spins at a low rate in relation to its forward motion, the surrounding air is fairly laminar. Stable laminar flow induces early separation of the boundary layer leading to a large wake field which induces an area of low pressure immediately behind the ball (incurring what is known as pressure drag). Not only does this affect the overall drag experienced by the sphere, smooth laminar flow has an adverse affect on lift as well. While backspin causes an area of low pressure above the sphere due to Bernoulli's Principle, a relatively low rotational velocity leads to an upward shift in the boundary layer, negating the lift due to Bernoulli's Principle and ultimately causing negative lift. This is known as the Reverse Magnus Effect. Consequently, low spin rates provide two drawbacks to trajectory: higher drag and reverse lift.
When the spin rate is high in relation to the forward motion, the surrounding air becomes turbulent. Turbulent airflow -- which normally increases drag on aerodynamic objects -- actually serves to increase airflow over the relatively non-aerodynamic sphere causing the boundary layer to follow the contour of the sphere's surface longer. (This is the same reason that golf balls have dimples, to induce turbulent flow which ultimately lowers the Reynolds number.) The turbulent airflow results in minimizing the wake field and ultimately diminishing the pressure drag. Additionally, the spin causes the boundary layer to experience a downward motion relative to the projectiles position. This leads to a net force of lift upon the sphere as the momentum shift of the boundary layer known as Magnus Lift. The higher the spin rate in relation to forward motion, the greater the area of lower pressure above the sphere and the greater the momentum shift, and thus the greater the effect of Magnus Lift.
Upon leaving the barrel, the pellet has a specific velocity and a specific rate of spin, which are translated into linear velocity (U) and rotational velocity (V), respectively. Additionally, both velocities begin exhibiting exponential decay as the linear velocity decreases due to the drag while the rotational velocity decreases due to surface friction. As the linear velocity decreases at a greater rate than that of the rotational velocity, the ratio of rotational velocity to linear velocity, V/U, grows.
A perfect friction exchange between the pellet and hop-up bucking would result in an initial V/U of 1. Although the friction exchange is very efficient, it simply is not possible to have a perfect friction exchange. Furthermore, the pellet has not reached its peak velocity as it makes contact with the hop-up bucking early in its transit through the barrel (though the rotational velocity will increase slightly as it spins down the barrel). For the majority of calculations, V/U was capped at 0.41. For a 0.20g pellet fired at 328 fps (or the equivalent of 1.00 Joule), a V/U of 0.41 would translate to a spin rate of 132,000 revolutions per minute. By comparison, a typical bullet leaves the barrel spinning at anywhere from 200,000 rpm to 300,000 rpm. For bullets, spin is directly proportional to the linear velocity and is easily calculated by multiply the muzzle velocity by the twist ratio. For instance, a .308" bullet might have a muzzle velocity of 2800 fps out of a rifle with a twist ratio of 1:8. In this case, it could have a spin of over 250,000 rpm. (Coincidentally, many bullets begin to suffer from instability issues due to structural failure of the jacket above 400,000 rpm.) While bullets are moving at much higher velocities than pellets, the pellets are significantly less dense and have a lower moment of inertia than that of bullets, which is why pellets are able to have such high spins imparted at relatively low velocities.
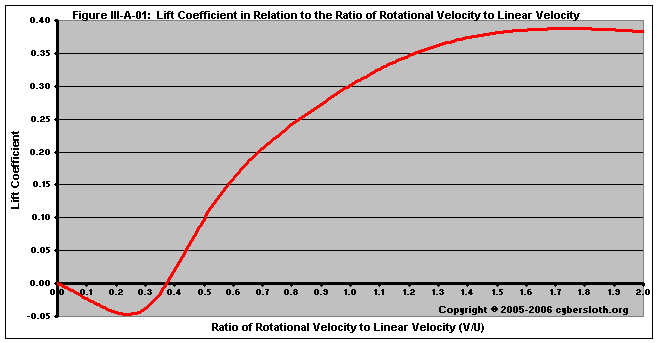
Figure III-A-01 illustrates the amount of lift generated proportional to the ratio V/U. Below a V/U of 0.37, the lift coefficient is actually negative -- anything below a ratio of 0.37 is subjected to the Reverse Magnus Effect. Above 0.37, lift is positive. Even if the pellet were to leave the barrel at a V/U less than 0.37, the linear velocity generally decreases at a greater rate than the rotational velocity, causing V/U to increase as the pellet follows its trajectory. If the rotational velocity were constant, the pellet would arc high into the air. An ideal hop-up setting will try to achieve lift coefficient that grows in relation to gravity (yet is not so high as to cause a high arc) thereby providing a seemingly flat trajectory.
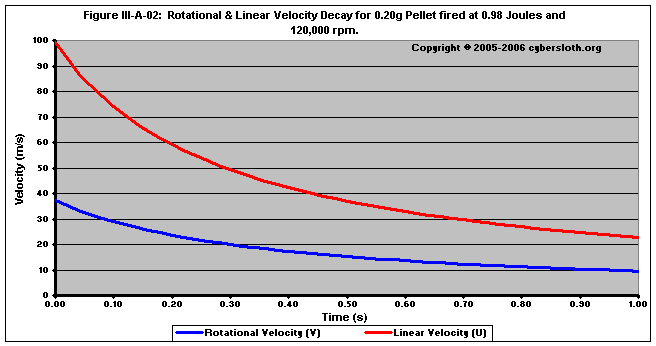
To explain how V/U affects the net vertical movement of the pellet, I have generated four plots that show how rotational velocity (V), linear velocity (U), the lift coefficient ( CL ), and net force experienced by a 0.20g pellet fired at 325fps with 120,000 rpm spin. In figure III-A-02, we can see how the linear velocity decreases rapidly (compared to the rotational velocity).
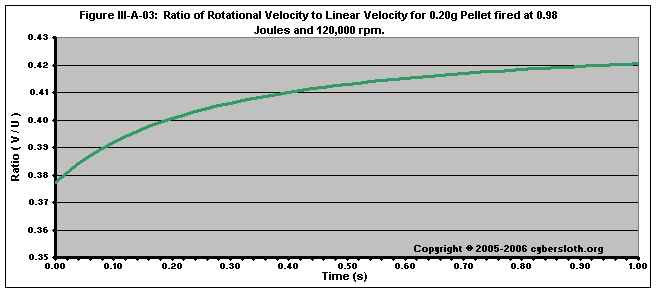
Since U decreases faster than V, we see the ratio V/U increase as depicted in Figure III-A-03.
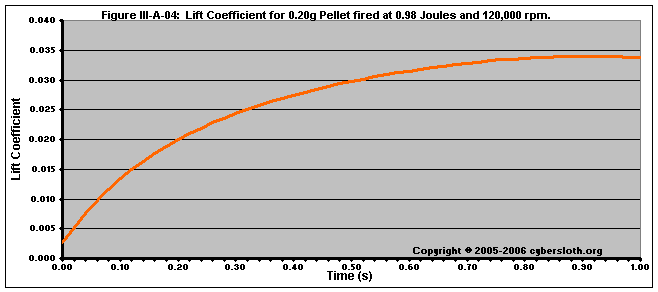
In Figure III-A-04, we can see how V/U contributes to lift, with positive lift being generated for quite a while. While the lift coefficient does steadily increase, the forward velocity (U) is decreasing rapidly which translates to a lower lift force at distance.
In Figure III-A-05, we can see how the opposing forces of lift ( FL ) and gravity ( Fg ) affect the overall vertical force ( Fy ) upon the pellet. For the first 0.04 seconds, the pellet is actually moving downward. For the next 0.26 seconds, the pellet is accelerating upwards. After 0.30 seconds (and a total distance of about 67 feet), the pellet begins a downward acceleration. Keep in mind that though the pellet is accelerating downwards, that does not mean that its velocity is downward but rather that it has a positive velocity that is quickly diminishing. The pellet does not start moving downward until after about 0.51 seconds have passed (or about 96 feet of distance).
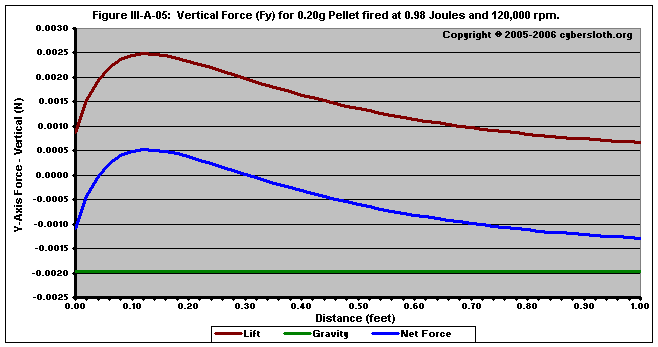
Figure III-A-06 shows the effects of hop-up upon a pellet. Notice that at 0 revolutions per minute (rpm) the pellet experiences a normal parabolic trajectory. At 36,000 rpm, V/U is low enough such that lift is negative due the Reverse Magnus Effect; since the force is negative (i.e., downward) it aids gravity in causing the pellet to fall. At 72,000 rpm, the Reverse Magnus Effect is higher still, causing a sharply downward trajectory. At around 100,000 rpm, the Magnus Effect begins to take effect causing positive lift, providing a trajectory closer to that of a BB fired without spin. At 115,000 rpm, the trajectory appears flat due to the effects of gravity being marginally negated due to the Magnus Force, while a higher rpm will cause the BB to arc skyward.
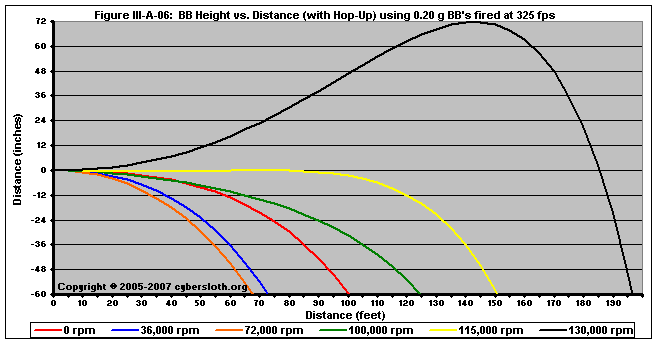
While the trajectory of the pellet appears to be nearly perfect out to 90 feet if fired at ~115,000 rpm, in reality the hop-up interaction doesn't always incur spin that is perfectly perpendicular to the ground along the z-axis (direction horizontally perpendicular to the rifle). Two reasons for this could be either the shooter holding the rifle with tilt or the pellet making a slightly off-center strike against the hop-up bucking.
Figure III-A-07 shows the effects of hop-up upon a 0.30g pellet fired at 407 fps. Again, we see the Reverse Magnus Effect cause degraded performance if hop-up is engaged yet not sufficiently high to generate a high V/U. It should also be noted that the plots are exaggerated along the y-axis -- while the degraded trajectory of shots fired with low hop-up are obvious on the plot, it would not be nearly so conspicuous in real observation. At 135,000 rpm, we see a relatively flat trajectory, while at 150,000 rpm we see a trajectory showing a greater arc above the aim point. While the 150,000 rpm shot will provide greater range, the 135,000 rpm would be more desirable as it would provide a flatter trajectory. Again, the axis is exaggerated -- the arc would not seem nearly so obvious in reality.
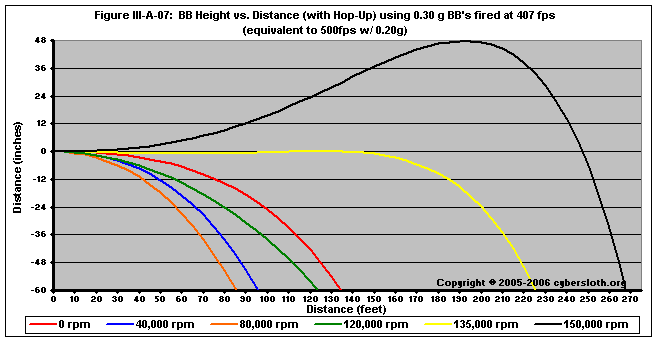
Figure III-A-08 depicts how an equal amount of spin affects various mass pellets when fired at equal energies. The reason that heavier mass pellets generate more lift is that, for equal muzzle energies, the heavier pellets have a lower linear velocity. This means that the ratio V/U is higher.
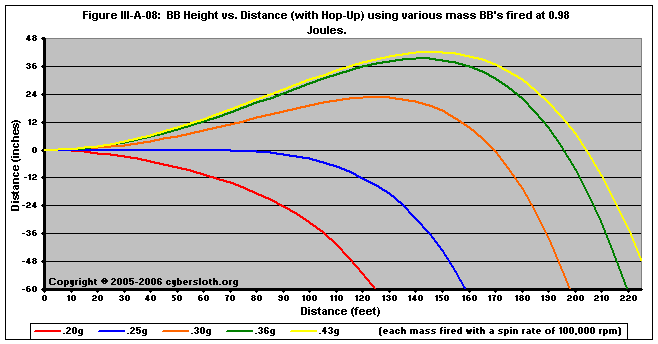
This information may seem contradictory at first. It appears as though a shooter would need to decrease the amount of hop-up when using heavier pellets, as opposed to reality wherein hop-up is normally increased when using heavier pellets. The problem lies in thinking that an unmodified hop-up setting would produce equal spin rates, however this is an incorrect assumption. Because heavier pellets will have a higher moment of inertia, more torque is necessary to generate an equal amount of spin. So while a particular setting may be fine for a 0.25g pellet, inserting a 0.30g pellet without modifying the hop-up will not generate enough torque to induce adequate spin on the 0.30g pellet. For example, a hop-up setting that results in 100,000 rpm of spin on a 0.25g pellet might generate only 80,000 rpm with a 0.30g pellet, as the heavier pellet striking the hop-up will not produce adequate torque to achieve the desired amount of spin.
Figure III-A-09 provides an estimate how a hop-up unit properly set for 0.25g pellets might produce sub par spin for the heavier pellet.
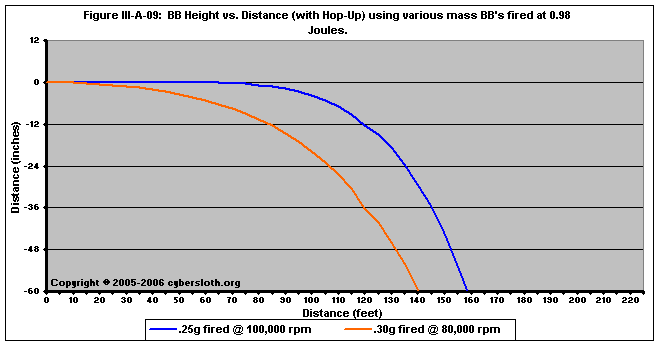
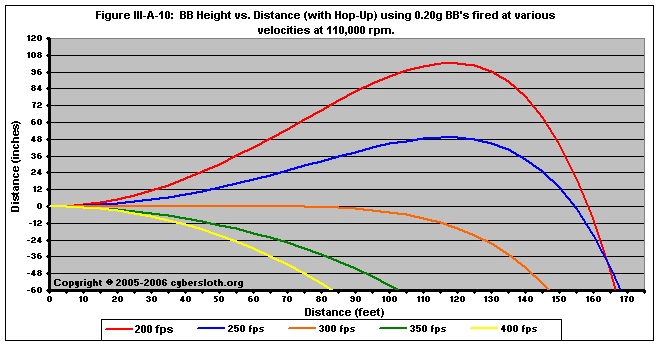
Figure III-A-10 shows how velocity affects trajectory when hop-up is applied. At lower linear speeds, V/U is high and results in a drastic, skyward arc in the pellet's trajectory. At higher linear speeds, the force of lift is insufficient as V/U is too low. It should be noted that, for equal hop-up settings, a higher muzzle velocity will result in higher spin rates (i.e., a hop-up setting that generates 95,000 rpm when a 0.20g pellet passes through at 300 fps might generate 125,000 rpm if the same pellet passed through at 400 fps), meaning that upgrading your gun will alter the trajectory, however it may not be as drastic as depicted below due to my use of consistent spin rates. I should note that a 200 fps shot with an initial spin of 95,000 rpm would have a very high V/U, and the trajectory depicted below for the 200 fps shot is probably impossible, as it would be very difficult to generate such high spin from a relatively low-energy shot.
Modeling trajectory in relation to hop-up proved to be a much more challenging task than any other factor contributing to trajectory. Calculating lift coefficients as well as the ratio of rotational velocities to linear velocities, and subsequently the Magnus Force, were key components that are reasonably easy to calculate. I had no luck in finding coefficients necessary to calculate the rate at which the spin drops off due to surface friction. Furthermore, collecting empirical data did not help as it was very difficult to achieve perfectly consistent results from a rifle's hop-up mechanism (most likely due to variance in muzzle energy from shot to shot), and visual observations were highly subjective; an observer would have a hard time discerning between a relatively flat trajectory and one that rose over 12 inches above horizontal at its apex.
Hop-up as modeled throughout these pages should not be taken as gospel -- they're very close but not perfect. One thing that was not taken into account in modeling hop-up is the diminished muzzle velocity due the energy loss from the pellet striking the hop-up rubber. This was initially going to be part of the model, however I could not determine direct correlation between spin and energy loss, particularly so considering that different rubbers seemed to have different effects with no uniform consistency. At any rate, while energy dissipation, velocity loss, and other things have been tested and verified, the hop-up model is theoretical and should be used as a guide to understand the relationship between velocity, mass, and spin; trying to use the hop-up model plots to estimate how much you should aim above a target at 200 feet is beyond the current limits of the model and should only be used with a grain of salt.