Section V-A-02: Crosswind Component
The crosswind component is taken as the wind component perpendicular to the line drawn from rifle to target. Just as was done with the headwind / tailwind component, the crosswind has to be reduced from the total wind component into a vector. This is done by taking the wind direction in relation to the original aim direction.
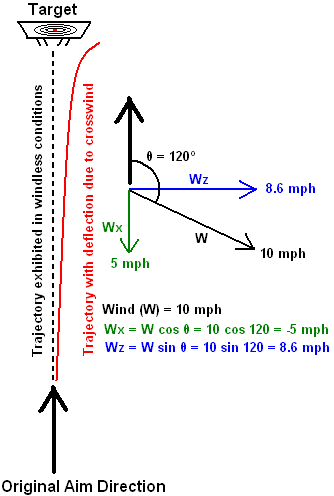
Figure V-A-02-a illustrates how to divide the wind direction into components. In this case, the wind is blowing at ten miles per hour at an angle of 120º to the direction aimed. This means that the BB will experience a headwind of five miles per hour and a crosswind of 8.6 miles per hour. For calculating the
|
deflection due to crosswind, we need only worry about the crosswind component, or 8.6 mph.
The next problem is determining how much wind affects the trajectory. This can easily be calculated by using the drag equation in Section I-D-01. The amount of deflection will be determined by the lateral velocity of the BB. In turn, the lateral velocity is dependent upon both how long the BB has been subjected to the crosswind and how fast the crosswind is moving in relation to the BB (or for how long and much of an acceleration the BB experiences..
Most people tend to adhere to either of two theories as to why a BB will or will not be affected by crosswind. The first theory is that the heavier BB's will retain their inertia better, thereby being less affected by a crosswind. As of such, the heavier BB will experience a lesser degree of deflection downrange.
The second theory is that all BB's, regardless of weight, will be "caught" by the wind and will be moving at roughly the same lateral speed as that of the medium that the BB's are passing through. |
Figure V-A-02-a: Wind Component
Diagram |
Most lay target shooters adopt this latter argument. This is understandable as it makes calculating wind deflection very easy. Additionally, most target shooters are dealing with a very dense projectile fired at a very high velocity.
Unfortunately, this latter theory is incorrect. Firearm and 0.177" BB shooters can get away with this to a slight degree because, again, they are dealing with a dense projectile moving at a very high velocity. For both bullets and steel BB's, the projectile reaches the target relatively quickly. Furthermore, the increased density (and mass) of both types of projectiles dictate that the force necessary to accelerate the projectile laterally must be significantly higher.
This IS NOT the case for airsoft shooters, however, as the projectile has a density much less than that of a bullet (or even a 0.177" steel BB) and the muzzle velocities tend to be considerably less for airsoft rifles when compared to the muzzle velocities of firearms and 0.177" BB guns. To illustrate this point, let's consider the following example:
Imagine that the shooter is firing at a target that is 100 feet downrange, and that he is firing a 0.20g BB at 275 fps into a a 20 mph crosswind. If the shooter estimates that the average velocity of the BB will be 160 feet per second (which is actually correct), then they can readily expect that it will take about 0.70 seconds for the BB to reach the target (again, the calculations reflect reality). If the BB maintains a constant lateral velocity of 20 mph (or about 30 feet per second) from the moment it leaves the barrel, then it would be deflected 21 feet to the side by the time it has traveled 100 feet. 21 feet is an awful lot -- I think that most airsoft shooters doing tests in such a crosswind would quickly determine that the lateral deflection is significantly less than 21 feet. In reality, the BB would only be deflected about 22 inches, a far cry from the 21 feet estimated earlier. Why the huge discrepancy? As will be illustrated below, the BB doesn't move at 20 mph upon exiting the barrel -- in fact, it doesn't even get close to 20 mph.
Figures V-A-02-b through V-A-02-e depict the lateral characteristics of different BB's that have been fired at 0.70 Joules (or the equivalent of 275 fps with a 0.20 g BB) into a 20 mph crosswind.
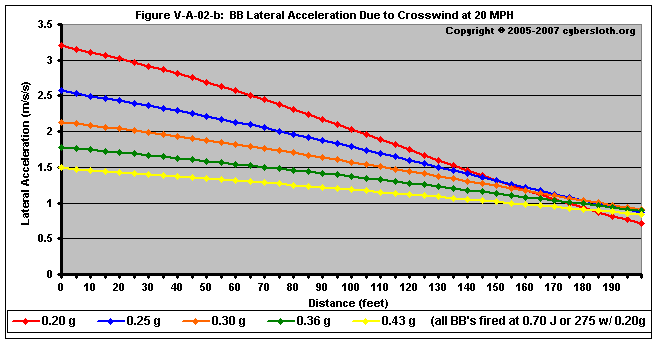
Drag acceleration is a function of mass, and as of such we would expect that BB's with a higher mass will experience a lesser acceleration. Figure V-A-02-b depicts lateral acceleration of a variety of BB masses. Consequently we see that the 0.20 gram BB's undergo a more pronounced acceleration due to the crosswind. Also notice that the acceleration decreases with time and distance. The reason that the acceleration decreases with time is that the BB is experiencing less drag with the passage of time. Think of it this way: when the BB leaves the barrel, it is subjected to drag that is a component of the wind velocity in relation to the BB. Immediately after leaving the barrel the BB is experiencing drag due to a lateral wind speed of 20 mph (or 8.94 m/s or 29.33 fps). As time passes, the BB begins to become a part of the moving medium. As this happens, the lateral wind speed in relation to the BB decreases, thereby reducing the lateral drag force.
In Figure V-A-02-c, we see the lateral velocity of the BB in miles per hour. Initially, all BB's have a lateral velocity of 0 mph. As time passes, the BB's gain velocity as they accelerate laterally. Notice that at 100 feet, the 0.20 gram BB will be moving laterally at about 4.1 mph. By contrast, notice that the 0.43 gram BB is moving laterally at about 2.2 mph. It is easy to see why heavier BB's fare better in higher winds than lighter BB's.
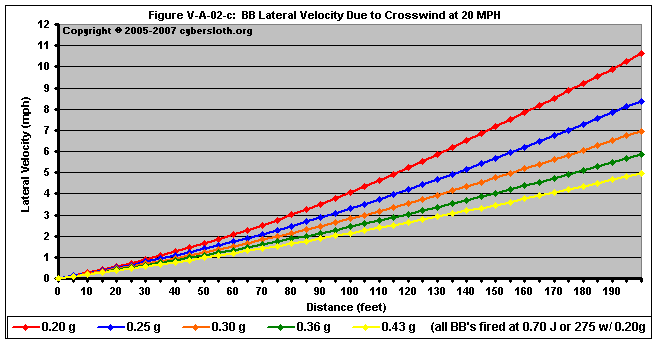
For the velocity graphic, I decided to show the lateral velocities out to a distance of 200 feet. The reason I did this was to illustrate that even the relatively light 0.20 gram BB will not reach a velocity of 20 mph at a distance of 200 feet. In truth, the projectile will never reach 20 mph as the lateral acceleration decreases steadily due to a continuously diminishing drag force. This might seem to contradict the fact that the the lateral acceleration is diminishing with time, however it only appears this way because the previous plot was generated as velocity versus distance. In a plot of velocity versus time, we can clearly see that the lateral velocity is decreasing, as is depicted in Figure V-A-02-d.
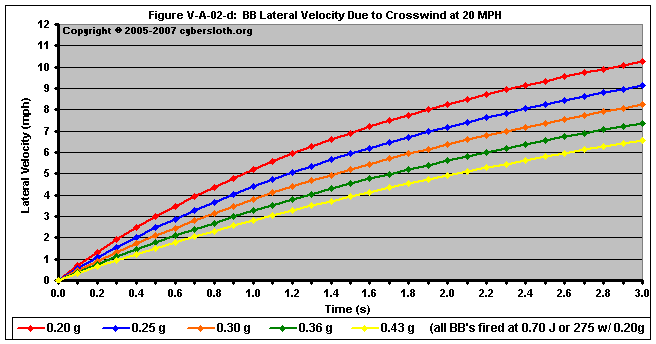
For the velocity vs time analysis, I decided to show the lateral velocities for a long model run of 3.0 seconds. This is completely academic, though, as it is impossible for a horizontally-aimed BB to stay airborne for three seconds. However, it does illustrate the fact that the projectile will not reach 20 mph after a very long flight time. Just for the sake of argument, I performed an extremely long model run out to 25 seconds. Here are the results:
| Time (seconds) | Velocity (m/s) | Velocity (mph) | |
| 0 | 0.00 | 00.0 | |
| 5 | 5.54 | 12.4 | |
| 10 | 6.84 | 15.3 | |
| 15 | 7.42 | 16.6 | |
| 20 | 7.75 | 17.3 | |
| 25 | 7.96 | 17.8 |
Again as the projectile's lateral velocity increases, the velocity of the wind in relation to the projectile decreases, reducing the amount of drag experienced by the projectile. Another model run that made calculations out to 50 seconds showed that the BB was still below 19 mph @ 50 seconds.
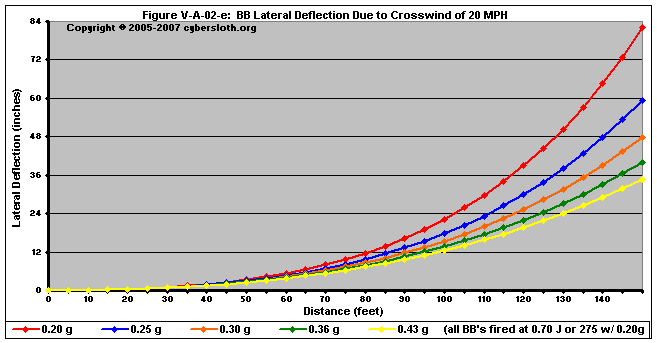
Finally in Figure V-A-02-e, we can see the actual deflection of the BB's. Even 0.25 gram BB's show a marked reduction in lateral deflection when compared to that of the 0.20 gram BB's. However, increasing the mass of the BB's became a law of diminishing returns. The difference in lateral deflection between a 0.30 gram BB and that of a 0.43 gram BB is only about four inches at a distance of 100 feet. And this is when fired at 275 fps. As we'll see, at higher velocities the differences between the masses becomes less at shorter distances.
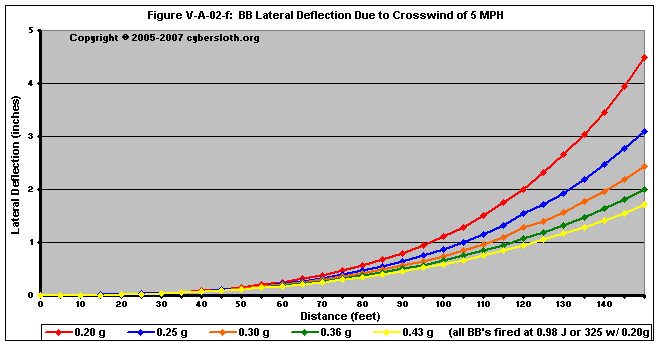
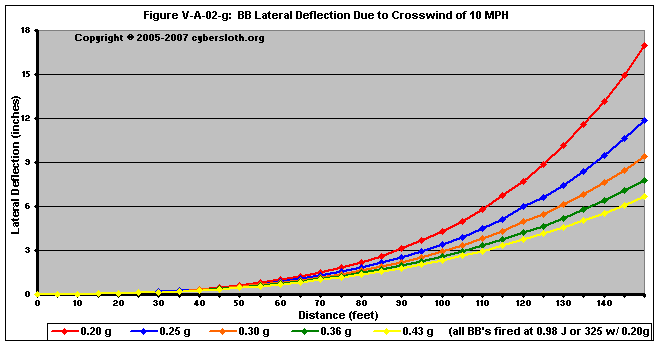
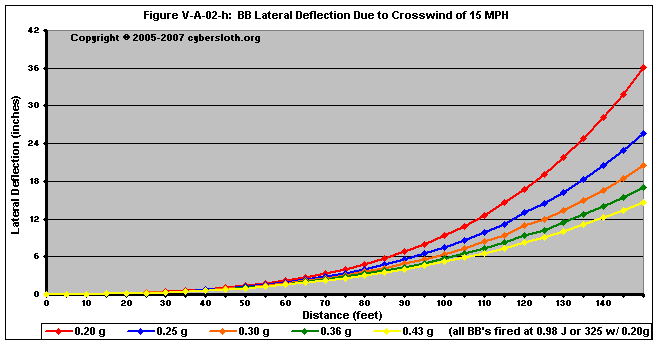
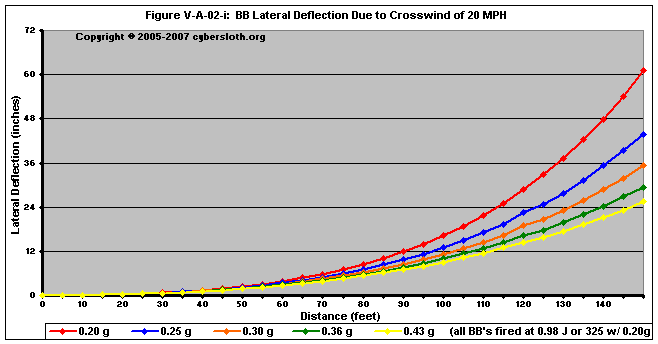
Figures V-A-02-f through V-A-02-i deal with projectiles fired at 0.98 Joules (or 325 fps with a 0.20g BB)
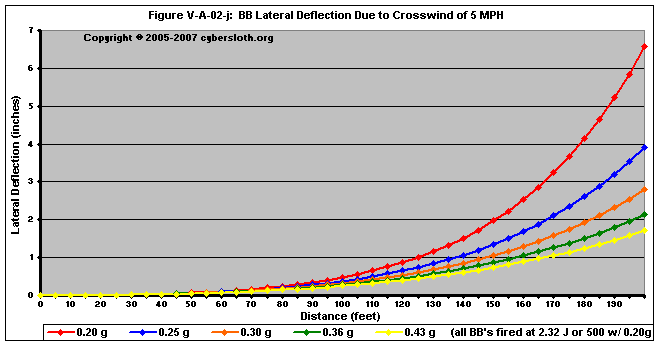
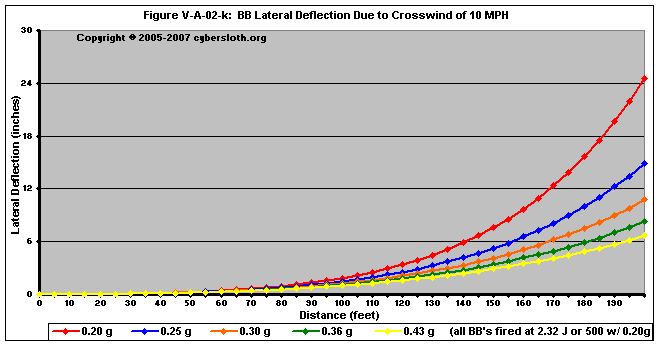
Figures V-A-02-j through V-A-02-m deal with projectiles fired at 2.32 Joules (or 500 fps with a 0.20g BB)
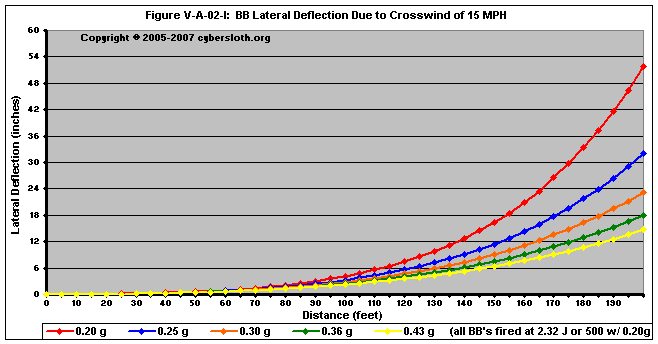
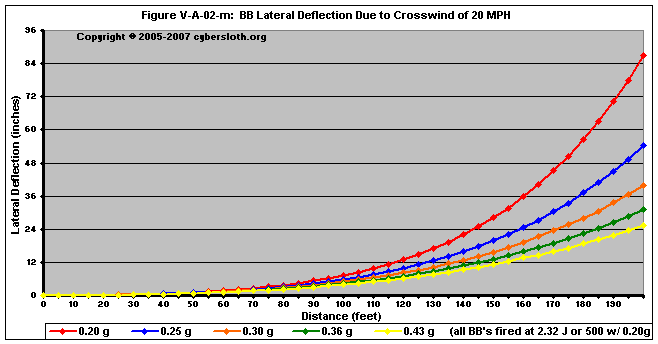
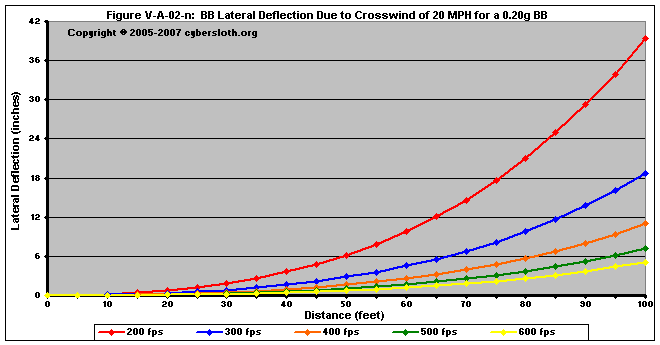
Lastly, Figure V-A-02-n shows how the relationship between muzzle velocity and crosswind. We can see that for equal BB weights, a high-power shot will reach its target having experienced less deflection. For instance, if you were firing at a target 100 feet away with a 20 mph crosswind, a 0.20g BB fired at 400 fps will have only been deflected about 11 inches, whereas a 300 fps shot would have been deflected around 19 inches.
Keep in mind that for an equal time period, the BB moves the same distance laterally for each shot. The high-power shots do not resist crosswind any better than the low-power shots; rather, the high-power shots get further down range in less time. To explain it further, the 600 fps shot reaches 100 feet after 0.32 seconds, after which time it has been deflected about 5 inches. After 0.32 seconds, the 500 fps shot has only gone 90 feet, where it has an equal deflection of 5 inches. By contrast, the 200 fps shot only reaches about 47 feet over the course of 0.32 seconds.