Section VIII: Closing Remarks
The study of the BB trajectories has been both challenging and interesting. There were a lot of questions that I didn't know the answer to when I set out to create the Airsoft Trajectory Project, and still other questions that I thought I knew the answer to, only to find out that I was wrong. It has taken a lot of testing, a lot of help, and a lot of communication to come up with the right model parameters. All in all, I'm fairly happy with the results as well as the learning process, and hope that others will find it useful too.
If you've waded through the data and haven't been able to figure out the answer to the initial questions posted on the introduction page, here they are again, complete with short (or as short as possible) answers and links to more in-depth explanations.
Is it worth upgrading a gun from x fps to y fps to get more range?
For equal muzzle energies, which BB goes further, 0.20g or 0.25g?
Which mass BB gets to the target the quickest for the given velocity?
Do heavier mass BB's have more energy than lighter BB's down range?
Is it necessary to restrict a rifle with a 600 fps muzzle velocity to a minimum engagement
What MED's are recommended to ensure both safety and fairness to all shooters?
Do 0.43 gram BB's negate the effects of wind that much better than 0.20 gram BB's?
Are people really able to achieve ranges out to 300 feet?
Do 8mm BB's provide better range than 6mm BB's?
Do 8mm BB's resist wind better than 6mm BB's?
Do high-velocity BB's resist wind better than low-velocity BB's?
Is it worth upgrading a gun from x fps to y fps to get more range?
There isn't a simple answer to this question... it ultimately depends on individual preferences. Hopefully all of the data will help you to determine whether or not it is worth upgrading.
For equal muzzle energies, which BB goes further, 0.20g or 0.25g?
One of the classic, seemingly never-ending debates that comes up is that of whether or not 0.20g BB's outrange 0.25g BB's. Given equal muzzle energies for BB's fired without hop-up, the heavier BB will always outrange the lighter one. There are two reasons for this: first, for a given equal muzzle energy, a lighter BB will have to be moving faster than the heavier one. Since the force of drag goes up exponentially with respect to velocity, a higher velocity will provide a much higher drag force than a lighter one. Which is to say that, for equal kinetic energies, the force of drag experienced by a lighter projectile will be much higher than it will be for a heavier projectile. Additionally, mass is an inverse component for calculating the deceleration due to drag. In other words as the mass of the projectile is increased, the deceleration due to drag is decreased thus extending range.
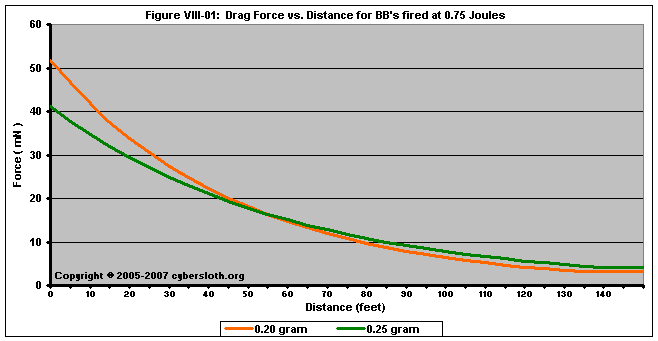
To illustrate this, here are charts depicting the deceleration and drag force experienced by a 0.20g and a 0.25g BB fired at 0.75 Joules (or 285 and 255 fps respectively). In Figure VIII-01, we can see that the drag experienced by the 0.20g BB is initially much greater than the drag experienced by the 0.25g BB. At about 53 feet, the drag force for both BB's are equal. This is simply because the drag equation does not take into account mass, but instead is primarily governed by velocity. At a distance of about 53 feet, both BB's are moving at about 165 fps, consequently they are experiencing the same drag force at that distance.
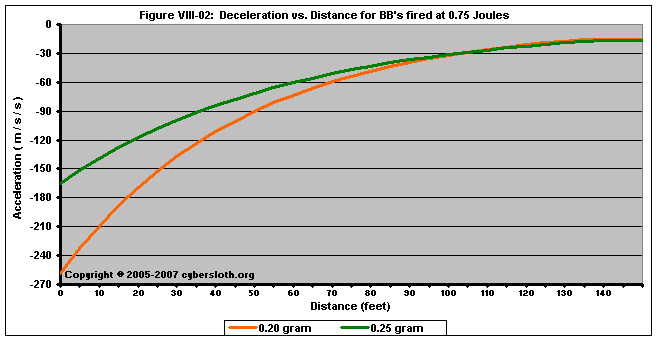
Acceleration, however, is dependent upon mass. Out until about 100 feet, the 0.20g BB experiences a greater deceleration than the 0.25g BB, and initially, the 0.20g BB experiences a deceleration that is 60% greater than that experienced by the 0.25g BB..
All of this may seem a little confusing because we're discussing both force and acceleration. To put it in perspective numerically, here are the calculations for instantaneous drag and instantaneous acceleration for three different BB's, Projectiles A, B, & C:
| Projectile | Mass | Velocity | Energy | Drag Force | Acceleration |
|
A |
0.20 g |
285 fps |
0.75 J |
52 mN |
-258 m /s2 |
|
B |
0.25 g |
255 |
0.75 |
40 |
-162 |
|
C |
0.25 g |
285 |
0.94 |
52 |
-206 |
Projectiles A & B are fired with equal energies. Because B has greater mass 0.25g, it achieves 0.75 Joules at a slower velocity compared to the 0.20g mass of A. Because B is moving slower, it experiences less drag force (which in turn contributes to a lesser deceleration). Note, however, that Projectiles A & C are moving at the same velocity (and because C has more mass, it has more energy). The drag forces, which are independent of mass, are equal for both BB's at the same velocity. The deceleration of C, however, is less because acceleration is a function of mass.
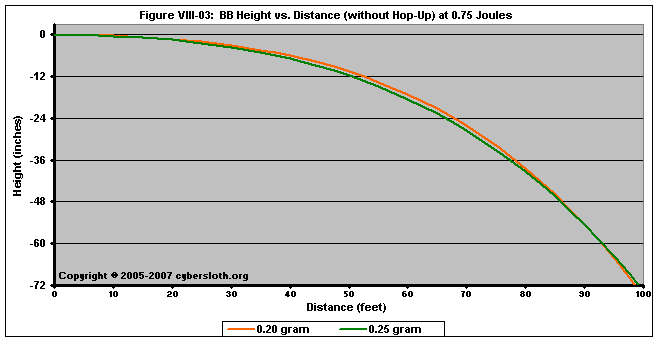
In Figure VIII-03, we can see that for non-spinning BB's, the 0.25g BB's eventually outdistance their lighter counterparts.. However, the thing that is most important to observe is that the difference is so small that it would be nearly impossible for the naked eye to observe.
When hop-up is applied, the lighter BB's are able to use backspin to generate lift more so than the heavier BB's. Of course, lighter BB's also lose spin faster than heavier ones, meaning that the effects of lift drop off rapidly down range. Ultimately, what happens is that both types of BB's experience similar trajectories.
In other words, there isn't an easy answer to the question of which BB goes further. Frankly, a lot of the answer comes down to semantics, namely what we describe as "effective range." In Figure VIII-04, we see the effects of hop-up on the same 0.20g and 0.25g BB's as above. If we consider "effective range" as the distance at which a BB experiences the least amount of deviation from the aim point out to 100 feet, then both BB's perform similarly. If a person is using a sniper rifle and is aiming at a target that is 140 feet away, and considers this the effective range for their sniper rifle by using holdover, then the 0.25g BB will travel further. Again, there isn't a clear answer, but rather depends on what the shooter defines as "effective range." (And... it would be hard to see a difference in trajectory between the two BB's as the trajectories are very similar.)
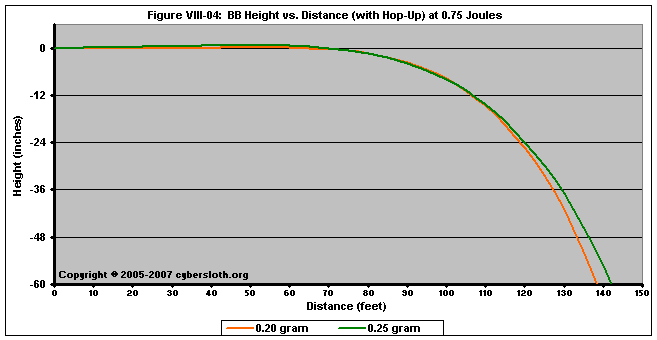
What is most important is that heavier BB's do not translate to a loss in range. At worst, the trajectory is on par with their lighter counterparts, and more often than not, heavier BB's will outrange lighter ones.
In Figure VIII-05, we see the trajectories of 0.20g, 0.30g, and 0.43g BB's fired at 2.32 Joules. At such a higher power, 0.20g BB's experience wild trajectories. If the shooter is aiming above their target at over 225 feet, 0.43g BB's do indeed go further, but it is the 0.30g BB that produce the desired trajectory.

A better example of the way in which heavier BB's outdistance lighter ones is to look at trajectories of a various masses fired at an angle above the horizon. Although of no practical importance, in Figure VIII-06 we can clearly see that heavier BB's do produce greater ranges.
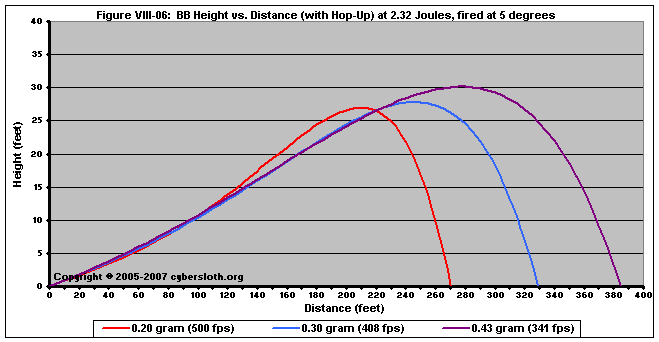
Ultimately, heavier BB's will outrange their lighter counterparts. This does not mean that heavier BB's are always the most useful or necessary ammunition.
Which mass BB gets to the target the quickest for the given velocity?
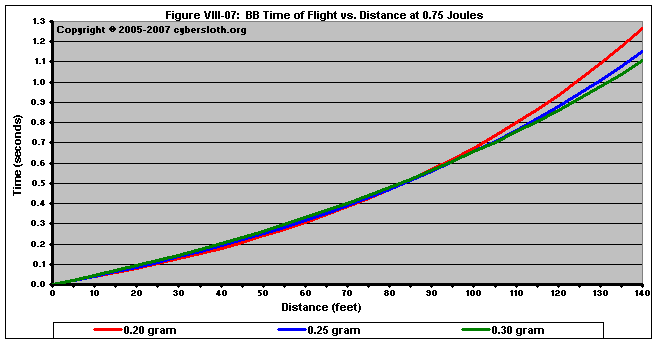
At ranges less than 100 feet, all BB's weighing between 0.20g and 0.43g get to their targets at roughly at the same time (assuming equal muzzle energies). In Figure VIII-07, we can see the flight times for various BB's fired at 0.75 Joules. All of them reach their targets at roughly the same time. For instance, a 0.20g BB reaches 70 feet in about 0.37 seconds, while a 0.25g BB reaches the same target in about 0.38 seconds, the time difference being hardly worth noting. At around 110 feet, we can see that the heavier projectiles are reaching their targets slightly faster. At 140 feet, a 0.25g BB would reach its target about 0.10 seconds faster than a 0.20g BB. Bit again, the difference is negligible.
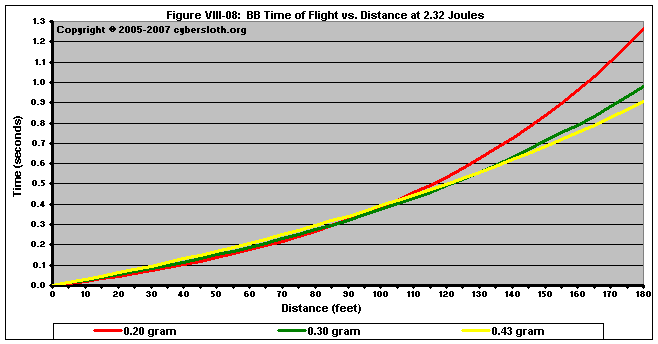
In high-powered rifles, the difference in time of flight is hardly noticeable at ranges less than 120 feet. In Figure VIII-08, we can see that the time difference only becomes really noticeable at 155 feet, where a 0.30g BB would reach its target roughly 0.20 seconds faster than a 0.20g BB. Again, this is noticeable on the chart, but 0.20 seconds goes by rather fast when being shot at.
So if you wanted a short and easy answer, it would be this
At ranges less than 125 feet, all BB masses reach their target at the same time if fired with equal muzzle energies. Beyond 125 feet, the heavier BB will usually get to the target faster than the lighter one.
Do heavier mass BB's have more energy than lighter BB's down range?
Determining which BB mass reaches its target the quickest or which BB mass goes furthest requires calculations and a complicated answer. Determining whether heavier BB's retain their energy better down range, however, has an easy and straight-forward answer that will always be true:
Assuming that a heavy and a light BB are being shot with equal muzzle energies, the lighter BB will always, always, always experience faster energy dissipation.
As was explained above, for a given muzzle energy a lighter BB will begin traveling faster. Because of this, it will decelerate much more rapidly compared to a heavier BB. We can see the energy dissipation in Figure VIII-09. In this case, we're looking at a various BB masses fired from a stock Tokyo Marui rifle with a muzzle energy of 0.75 Joules (with the 0.20g fired at 285 fps, the 0.25g fired at 255 fps, and the 0.30g fired at 233 fps). Notice that the heavier BB's retain their energy much better.
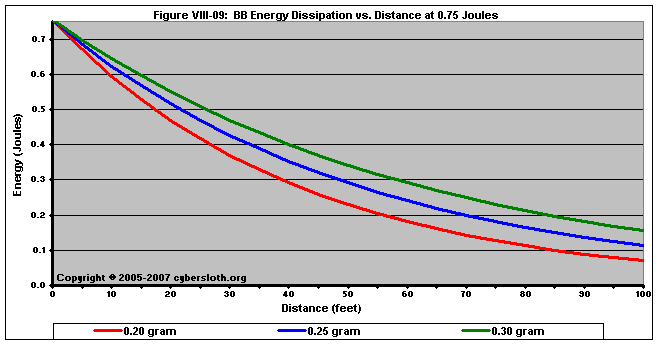
This is very important when determining safe engagement distances, and is explained in greater detail in Section VI: Minimum Engagement Distance.
Keep in mind that this only holds true when comparing 6mm BB's to other 6mm BB's. The area normal changes when talking about 8mm BB's, however a 0.34g 8mm BB will always lose energy much more rapidly compared to a 0.45g 8mm BB.
Is it necessary to restrict a rifle with a 600 fps muzzle velocity to a minimum engagement
distance of 100 feet?
As was discussed above (and discussed very thoroughly in Section VI-C: Recommended Universal MED's), it all depends on what BB the shooter is using.
Let's take the example of a rifle firing at 3.35 Joules, with energy dissipation depicted in Figure VIII-10. If a site wishes to base their MED's using a maximum impact energy of 1.00 Joules, then a shooter firing a 0.20g BB at 3.35 Joules (or 600 fps) would need an MED of only... 50 feet. However, if the same shooter were firing a 0.43g BB at 3.35 Joules (or 409 fps w/ 0.43g), then the MED would need to be extended out to... 108 feet, over twice the distance needed for the 0.20g shot.
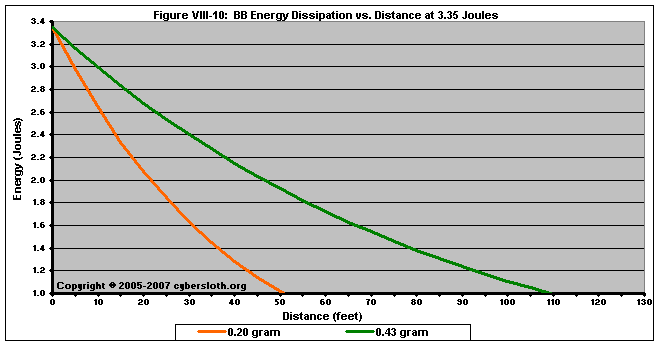
The main reason that I divide MED's based on BB weight is that weight (or mass, technically, but you know what I mean) makes a huge difference in energy dissipation. If a site wishes to enforce an MED for rifles that chrono at 500 fps with 0.20g BB's, then they could either restrict the MED to 80 feet for any BB weight, or use an MED of 55 feet and restrict the maximum weight of the BB's to 0.30g (though all snipers would be on the "honor system" in terms of ensuring that they do not use a BB weight above 0.30g).
To see how different BB weight classes translate to different MED's, use the calculator provided in Section X-B: Relative Energy / MED Calculator. Even a 1.49 J rifle (400 fps w/ 0.20g) has different MED's whether using 0.20g or 0.25g BB's.
What MED's are recommended to ensure both safety and fairness to all shooters?
Again, it is a complicated answer, however it is answered in full in Section VI-C: Recommended Universal MED's, complete with printable charts. If you have any questions, or would like advice or custom charts for your site, feel free to contact me.
Do 0.43 gram BB's negate the effects of wind that much better than 0.20 gram BB's?
This is another easy one. Heavier BB's always hold their trajectory better than lighter ones in the wind. They do so for the reasons discussed above wherein we learned that acceleration is inversely proportional to mass. As the mass of the projectile increases, the lateral acceleration decreases meaning that heavier BB's will experience less drift compared to lighter ones. This is explained in detail in Section V-A-02: Crosswind Component and is further depicted below in FigureVIII-11.
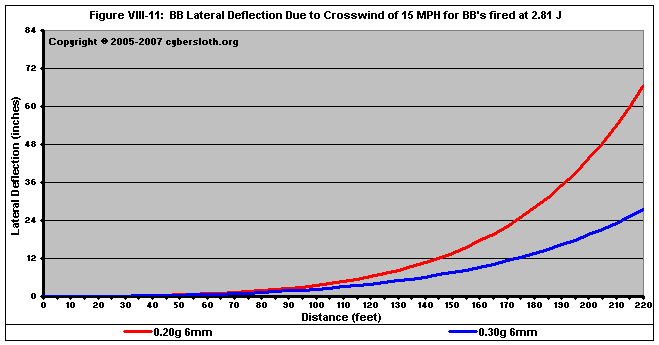
Here we can see the effects of a 15 mile per hour crosswind on a 2.81 Joule rifle. At a range of 220 feet, a 0.30g BB will have drifted a little over two feet lateral to the target, whereas a 0.20g BB will have been deflected over five feet lateral to the target. Going to progressively heavier-mass BB's would produce even less lateral deflection, however it would observe a law of diminishing returns, as is shown in Section V-A-02: Crosswind Component.
Are people really able to achieve ranges out to 300 feet?
In short, it is definitely possible to hit something at 300 feet.
Having worked through the problem in terms of theory and some testing using my own rifle, it is very possible to hit something at 300 feet and airsoft snipers are indeed achieving "kills" at that range and beyond. That being said, I'm still pessimistic in that I doubt that a shooter could routinely hit a target at that range. The longest range that I have achieved, observed, or have had verified for hitting at a 18" diameter target consistently is 235 feet. That is not to say that further engagements are impossible, but rather that this is the highest effective range that I have observed first-hand. Your mileage may vary...
If a shooter has a highly-upgraded rifle, he can extend his range out to 300 feet by aiming above the target. Take for example a shooter with a 3.35 J rifle firing at a target 300 feet away. Figure VIII-12 shows the trajectory of a 3.35 J shot using 0.36g BB's. In this case, the shooter would need to aim nearly seven feet above their target. Again, the rifle would have to be very consistent, and the shooter would probably need luck on their side, but it is definitely possible. (And... a 300' shot would be highly, highly unlikely with either a 0.20g or 0.25g BB.)
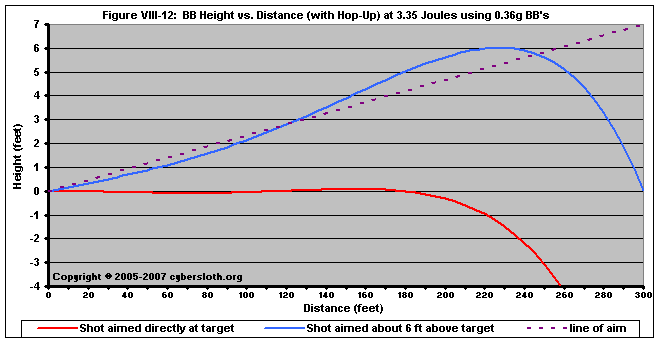
Another thing that a shooter should realize is that the impact energy at 300' will be greatly, greatly reduced. In the case of the 3.35 J rifle firing a 0.36g BB, the impact energy of that shot at a range of 300' would be about 0.06 Joules. In our tests, we found that BB's hitting a target at 0.06 Joules bounced off of standard sheet of paper (typically without leaving even a mark) and would be all but impossible to feel.
Do 8mm BB's provide better range than 6mm BB's?
The short, simple answer is "nope."
However, like most things, this is a subject that requires a little interpretation. First up is a comparison of BB's fired at 2.32 Joules, the equivalent of 500 fps with 0.20g BB's. For the examined BB's, this would be equivalent to 408 fps with the 0.30g 6mm, 384 fps with 0.34g 8mm, and 333 fps with 0.45g 8mm. Figure VIII-13 depicts the trajectories:
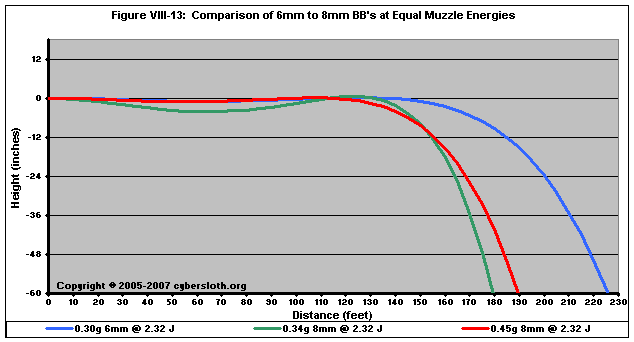
It is fairly obvious that, for equivalent muzzle energies, the lighter 6mm BB actually produces greater range. More specifically, the 6mm BB goes about 25 feet further than the 0.45g 8mm BB, and about 30 feet further than the 0.34g 8mm BB.
One thing that needs to be considered here is the fact that 8mm BB's dissipate velocity -- and consequently energy -- at a much faster rate than 6mm BB's. In other words, the 6mm BB's in the above case require greater MED's. The 0.30g 6mm BB would need an MED of 53 feet, whereas the 0.45g 8mm BB would need an MED of 45 feet, and the 0.34g 8mm BB would need an MED of only 38 feet.
One problem that I see throughout U.S. sites is that 8mm BB's are given equivalent, or in some cases greater, MED's when compared to 6mm BB's. Imagine a site that restricts muzzle velocities to lower than 500 fps, and gives an MED for those rifles of 55 feet. An airsoft player shows up with an 8mm rifle that fires a 0.34g 8mm BB at 487 fps (a whopping 3.75 Joules). Most sites would not allow this rifle on the site. In reality, if the site considers a 500 fps rifle fine with an MED of 55 feet, then the 487 fps would be just as safe with the same MED; at 55 feet, both would have an impact energy of 1.00 Joule (and the 8mm BB would ultimately be safer still because the energy is dispersed over a greater area). (To learn more about MED's, and to see recommended MED's based on muzzle energy, BB weight and size, consult Section VI-C: Recommended Universal MED's).
All of that is to say that comparing 6mm BB's to 8mm BB's based on muzzle energies puts the 8mm BB's at an unfair disadvantage. (And keep in mind that I am not an 8mm shooter, and do not make these statements based on bias but rather on an effort to ensure both safety and fairness in airsoft.) A better comparison of 6mm BB's to 8mm BB's would be one based off of the MED's imposed.
As previously stated, a 500 fps rifle firing 0.30g 6mm BB's would have an MED of 55 feet. For a 0.34g 8mm BB to have an MED of 55 feet, it would need to be fired at 487 fps (3.75 J), and a 0.45g 8mm BB would need to be fired at 360 fps (2.71 J). Figure VIII-14 depicts the trajectories of the three BB's.
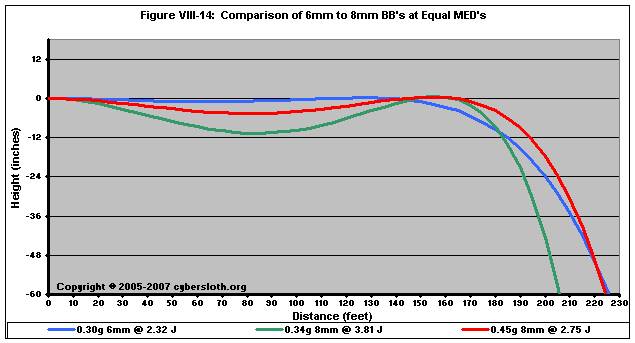
Even with equal MED's, the 6mm BB still outperforms the 8mm BB's, however both are a lot closer now. Because 8mm BB's are more consistent and require lower spin due to the hop-up to achieve the desired trajectory (and because 8mm BB's are less likely to fly errant due to surface imperfections), the 8mm BB's would achieve greater consistency in the terminal phase of their trajectories. Even so, given the added range (and precision standard of some high-grade 6mm BB's), I would consider the effective range of 6mm BB's to always be greater than that for 8mm BB's.
Do 8mm BB's resist wind better than 6mm BB's?
For the same reason that 8mm BB's dissipate velocity at a much greater rate than 6mm BB's, 8mm BB's also experience greater lateral deflection due to a crosswind. One thing to keep in mind is that 8mm BB's are less dense in comparison to 6mm BB's (for specifics, see Section I-A-02: Density/Volume). Additionally, the greater sail area of the 8mm BB's means that the lateral drag due to wind is going to be higher than that for 6mm BB's.
Figure VIII-15 depicts the lateral deflection of various 6mm and 8mm BB's fired at 2.81 J in a 15 mile-per-hour cross wind.
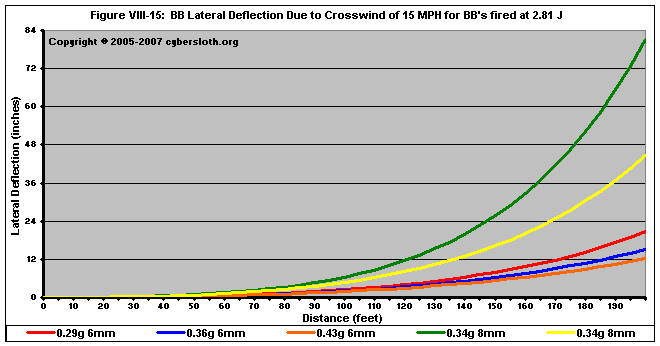
At a range of 200 feet, the 6mm BB's have only been deflected between one and two feet from the aimpoint. The 0.45g 8mm BB, by comparison, has been deflected nearly four feet, and the 0.34g 8mm BB has been deflected nearly seven feet. Even if you were to compare the 0.45g 8mm BB to a 0.20g 6mm BB, the 0.20g 6mm still holds it's trajectory better in terms of lateral deflection (the 0.20g 6mm BB deflection is above).
In brief, 6mm BB's resist the effects of crosswind MUCH better than 8mm BB's.
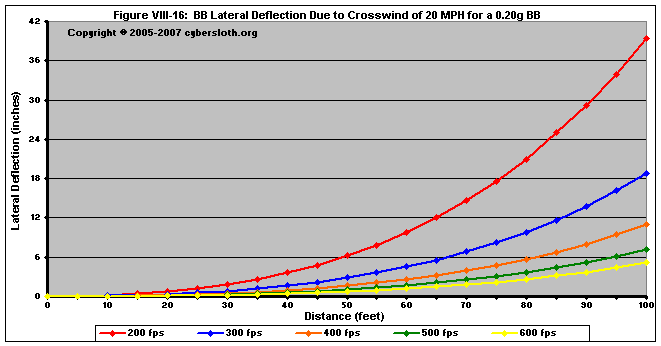
Do high-velocity BB's resist wind better than low-velocity BB's?
High-velocity BB's DO NOT resist wind any better than low-velocity BB's. Rather, high-velocity BB's reach their target faster than low-velocity BB's, meaning that there is less time for the wind to deflect a high-velocity BB.
To better explain it, here is a graph with text taken directly from Section V-A-02: Crosswind Component:
Figure VIII-16 shows how the relationship between muzzle velocity and crosswind. We can see that for equal BB weights, a high-power shot will reach its target having experienced less deflection. For instance, if you were firing at a target 100 feet away with a 20 mph crosswind, a 0.20g BB fired at 400 fps will have only been deflected 11 inches, whereas a 300 fps shot would have been deflected around 19 inches.
Keep in mind that for an equal time period, the BB moves the same distance laterally for each shot. The high-power shots do not resist crosswind any better than the low-power shots; rather, the high-power shots get further down range in less time. To explain it further, the 600 fps shot reaches 100 feet after 0.32 seconds, after which time it has been deflected about 5 inches. After 0.32 seconds, the 500 fps shot has only gone 90 feet, where it has an equal deflection of 5 inches. By contrast, the 200 fps shot only reaches about 47 feet over the course of 0.32 seconds.